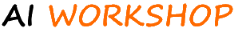Nie tak miało być, ale widzę, że prawie cały rok przyszło czekać na nastepny wpis. Na szczęście nie jest to poczytny periodyk (jeszcze ;-) ). Jeśli ktoś poza mną czekał na ten moment, to z góry przepraszam za opóźnienie. Lecimy z tematem. O co chodzi z tymi żabami?

Żaby

Wspomniane w tytule żaby to nawiązanie do książki, którą w 1959 roku napisało kilku panów. Książka ta to "What The Frog's Eye Tells The Frog's Brain". Została on napisana przez Jerome Lettvina, H.R. Marurana, Warrena McCullocha oraz Waltera Pittsa. Traktuje ona o włóknach łączących oko i mózg żaby. Jednak nie żaby nas interesują, ale dwóch ostatnich współautorów tej książki (chociaż niektórzy podają, że nie są oni jej współautorami, a jeden z nich przez nią spalił swój doktorat).

McCulloch i Pitts opracowali i przedstawili pierwszy model sztucznego neuronu w 1943 roku. Na początku był to model bardzo prosty podobny do tego do czego doszliśmy na końcu poprzedniego wpisu. Dla przypomnienia - doszliśmy wtedy do ładnego wzorku:

Model tych panów zakładał binarne wartości na wejściach i wyjściach oraz pewną elastyczność co do wartości progu aktywacji. Jako fukcje aktywacji używał bardzo prostej fukcji schodkowej Heaviside'a. Jest to fukcja o dwóch możliwych wartościach (jak się pewnie spodziewasz): 0 i 1. Dla argumentów ujemnych przyjmuje ona wartość 0, a dla pozostałych 1.

Funkcja ta występuje jeszcze w wariantach z wartością 0 lub 1/2 dla x równego 0, ale zostańmy przy pierwszym, najprostszym wariancie.

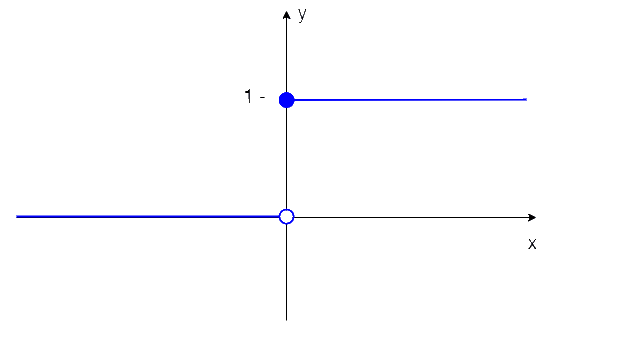
Taki prosty neuron może być użyty do budowy najprostszej sieci neuronowej - perceptronu. I teraz spróbujemy sobie takie cudeńko zakodzić.

Śliwki

Jest takie polskie przysłowie "pierwsze śliwki robaczywki". Mam nadzieję, że w moim przypadku nie będzie za dużo robaków (bug-ów).

Co sobie zakodujemy? Spróbujemy od czegoś najprostszego, aby ruszyć z tematem. Jak to mówią najtrudniej jest zacząć. Także pierwsze trzy neurony będą nam realizować trzy podstawowe funkcje logiczne (o których było ostatnio: alternatywę, koniunkcję oraz negację). Trzy neurony - znaczy jeden do każdej funkcji (a nie sieć trzech neuronów). Zaczynamy więc od najprostszego z możliwych perceptronów.

Dla naszych funkcji mamy do dyspozycji jedno lub dwa wejścia. Wartości na nie podawane będą oczywiście zerem lub jedynką. Mamy także dwie lub trzy (liczba wejść plus bias) synapsy, które będą miały przypisaną jakąś wagę (w0, w1, w2). Skąd weźmiemy jej wartość? Moglibyśmy ją ustalić arbitralnie. Jeśli chcesz możesz pomyśleć przez chwilę jakie mogą to być wartości w przypadku każdej z funkcji. Nie zapomnij proszę o funkcji aktywacji (funkcji Heavisida), która jest na wyjściu neruonu. Skąd te wartości weźmie komputer? Dla niego przyjmę na początek inne podejście. Napiszemy krótki program, który będzie działał według następującego algorytmu uczącego (na początku bardzo topornego):

1. użyjmy zmiennej W, której wartość ustalmy na początek na 0
2. dla każdej możliwej kombinacji wag o wartościach od -W do W:
• sprawdź czy neuron podaje prawidłowe wyniki dla wszystkich możliwych argumentów
• jeśli tak -> możemy wyjść - otrzymaliśmy nauczony neuron
• jeśli nie -> zwiększ W o 1 i wracamy do punktu 2

Może się zastanawiasz dlaczego tak a nie inaczej działa ten program i po co to W. Chodziło mi o to aby otrzymane wartości wag było możliwie bliskie zeru. Dodatkowo przy tak małej liczbie kombinacji można neuron nauczyć metodą "brutalną" (sprawdź wszystkie możliwości).

Mięsko

Jesteśmy coraz bliżej kodu. Rączki już chcą "ifować". Napiszę jeszcze kilka założeń dotyczących programu. Program będzie napisany w czymś, co wydało mi się najprosztszym rozwiązaniem na początek. Używał będę języka C# oraz .NET Core. Mogłaby to być również popularniejsza Java lub Python, ale myślę, że na początek nie ma to znaczenia. Co do formy programu to będzie to zwykła "konsolówka".

Moje przykładowe programy będę umieszczał pod adresem: https://github.com/TomaszChudak/Kutokasta. Dzisiaj mamy do czynienia z wersją 0.1 dostępną w katalogu Kutokasta-0.1

Opiszę teraz ją pokrótce. Główną klasą jest tutaj: LearningDispatcher. On z kolei korzysta z trzech kolejnych. Na początku z LearningSetReader, która będzie na początku czytać wszystkie pliki *.json z katalogu "LearningSets". Każdy z nich zawiera opis jednej fukcji. Pliki te wyglądają następująco:

   
                                        {
"name": "logical disjunction",
"examples": [
    {"input": [0, 0], "output": 0},
    {"input": [0, 1], "output": 1},
    {"input": [1, 0], "output": 1},
    {"input": [1, 1], "output": 1}
]
}                                        
                                    

   
                                        {
    "name": "logical conjunction",
    "examples": [
        {"input": [0, 0], "output": 0},
        {"input": [0, 1], "output": 0},
        {"input": [1, 0], "output": 0},
        {"input": [1, 1], "output": 1}
    ]
}                                        
                                    

   
                                        {
    "name": "logical negation",
    "examples": [
        {"input": [0], "output": 1},
        {"input": [1], "output": 0}
    ]
}                                        
                                    

Myślę, że zawartość tych plików jest oczywista - mamy tutaj prosty json z dwoma polami:

• name - które zawiera nazwę funkcji, której będziemy chcieli nauczyć nasz neuron ("logical conjunction" czyli koniunkcja)
• examples - tabelę z możliwymi przykładami (np. 4 możliwości) i dla każdego z przykładów: argumenty wejściowe - w tabeli (np. "input" równe "[0,0]") oraz wartość wyjścia (np. "output" równe "0").

Po wczytaniu plików z przykładami uczącymi program stara się znaleźć możliwe rozwiązanie. Będzie za to odpowiedzialna klasa: WageFinder. Jej główna metoda: GetWorkingWages realizuje opisany powyżej algorytm programu. Wygląda ona następująco:

   
                                        public WageSet GetWorkingWages(LearningSet learningSet)
{
    var reasonableWageSets = _wageLimitProvider.GetReasonableWageSets();

    foreach (var wageSet in reasonableWageSets)
    {
        var rightAnswersCount = GetRightAnswersCount(learningSet, wageSet);
        if (rightAnswersCount == learningSet.Examples.Count())
            return wageSet;
    }

    return null;
}                             
                                    

Na początku _wageLimitProvider dostarcza nam (leniwą kolekcję) możliwe kombinacje wag. Potem dla każdej kombinacji sprawdzamy czy wszystkie przykłady uczące dają poprawną odpowiedź (liczba poprawnych odpowiedzi jest zgodna z liczbą przykładów). Jeśli tak to zwracamy taką kombinację (jeśli nie null). Na szczęście dla naszych prostych przykładów szybko dostajemy wyniki.

Są one wyświetlane (jak się nietrudno domyśleć przez klasę ResultDisplayer) na ekran. Poniżej przedstawię jak one wyglądają oraz jak wygląda neuron realizujący daną funkcję.

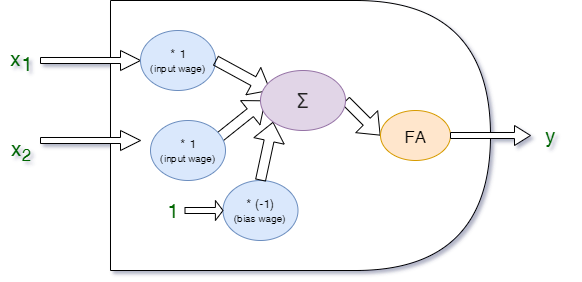
Alternatywa:

   
                                    Function: logical disjunction
Working wages are:
Input Wages:1
Bias Wage:-1                             
                                

Sprawdźmy przykładowo jak będzie wyglądać obliczanie wyniku dla wartości: x1 = 0 oraz x2 = 1. Dostajemy wtedy do zsumowania wartości: (0 * 1) + (1 * 1) + (1 * -1) co daje nam sumę: 0 i po przetworzeniu przez funkcję aktywacji 1 na wyjściu. Czyli to czego się spodziewaliśmy.

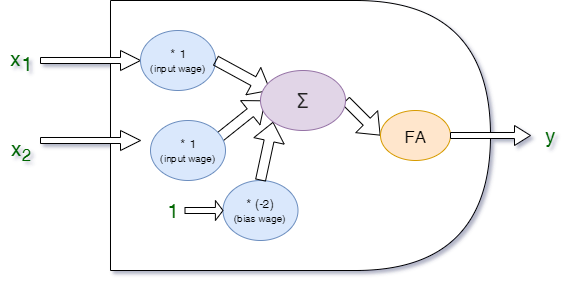
Koniunkcja:

   
                                    Function: logical conjunction
Working wages are:
Input Wages:1
Bias Wage:-2                             
                                

Tutaj również zobaczmy jak będzie wyglądać obliczanie wyniku dla wartości: x1 = 0 oraz x2 = 1. Dostajemy wtedy do zsumowania wartości: (0 * 1) + (1 * 1) + (1 * -2) co daje nam sumę: -1 i po przetworzeniu przez funkcję aktywacji 0 na wyjściu. Czyli to czego się spodziewaliśmy. Dopiero przy obu wejściach równych 1 "dobijemy" do sumy równej: 0 co da nam: 1 na wyjściu.

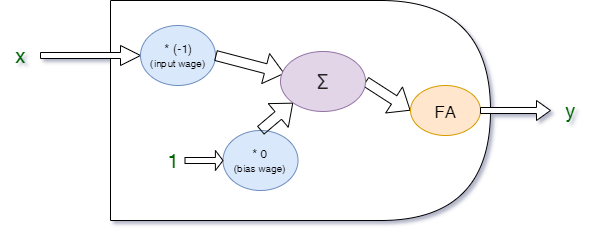
Negacja:

   
                                    Function: logical negation
Working wages are:
Input Wages:-1
Bias Wage:0                             
                                

Dla negacji sprawa jest jeszcze prostsza. Waga biasu ma wartość 0 więc można ją pominąć przy sumowaniu. Dla wejścia równego: 0 dostajemy sumę równą: 0 co daje nam: 1 na wyjściu. Dla wejścia równego: 1 dostajemy sumę równą: -1 co daje nam: 0 na wyjściu. Czyli ładna negacja :)

Finito

To tyle na dzisiaj. Na razie wygląda pięknie. Jak pewnie dało się zauważyć dzisiaj wszystkie realizowane przez nas funkcje były symetryczne, więc ta sama waga mogła być zastosowana do wszystkich wejść neuronu. A czy tak otrzymaliśmy już program, który może zrobić wszystko? To już sie okażę w następnym wpisie.

Na dzisiaj mogę dodać jeszcze, że mieliśmy do czynienia z metodą uczenia nadzorowanego. Możesz o tym sobie przypomnieć tutaj. Do następnego razu.