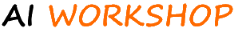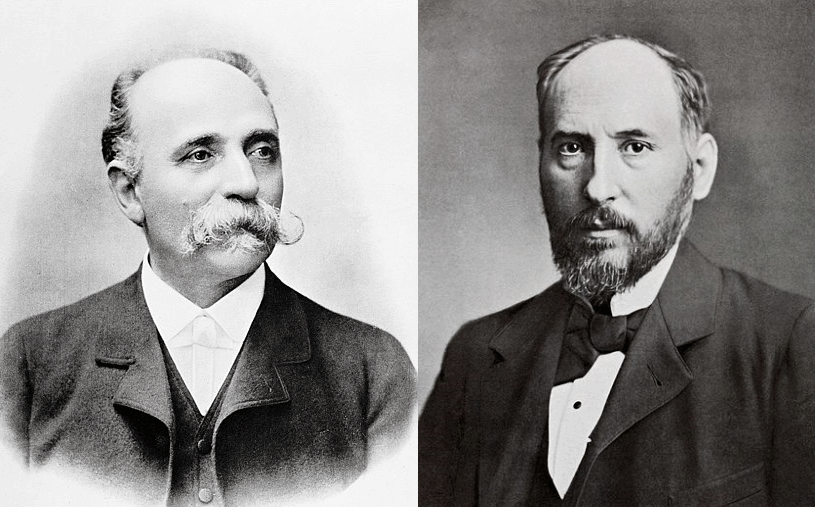Dzisiaj miała być obiecana porcja mięska (pierwszy kod). Jednak wpis wyszedł całkiem długi i bez tego więc mięsko będzie związane tylko z biologią. Lecimy.
Dawno dawno temu, ale też w XIX wieku uważano nasz kochany mózg za jednolitą masę. Na szczęście świat posiada wielu ciekawskich, którzy nie zatrzymują się tam gdzie stoją i próbują coś zbadać, obejrzeć, pokroić, sprawdzić. Do takich ludzi należał Włoch Camillo Golgi (na obrazku powyżej po lewej stronie), który już w XIX wieku opracował "czarną reakcję" (jak ją nazywał) czyli metodę barwienia preparatów. Metoda ta polegała na naprzemiennym użyciu kilku odczynników i suszeniu kawałka tkanki. Bazowała na podobnych metodach stosowanych wtedy w fotografii. Dzięki temu możliwe stało się takie przygotowanie preparatu, że mając mikroskop można było zaobserwować neurony.
Dzięki tej metodzie Hiszpan Santiago Ramón y Cajal (na obrazku powżej po prawej stronie) mógł bez przeszkód kroić, przygotowywać i badać tysiące zwierzątek i skutecznie badać ich mózgi. Poczynił on ważne odkrycie dotczyące neuronów. Zauważył, że aksony kilku neuronów nie są ze sobą połączone. Łączą się za to z dendrytami innych neuronów. Mamy więc do czynienia ze swego rodzaju uporządkowaną siecią. Ale zanim przejdziemy do całej sieci zatrzymajmy się na chwilę przy neuronie.

Neuron

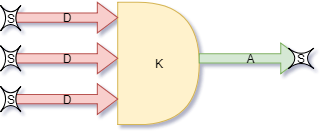
W naszej głowie mamy ich miliardy. Ich bodowę wewnętrzną poznaliśmy już na tyle, że możemy rozpoznać w nich wiele skomplikowanych elementów wewnętrznych. Jednak dla potrzeb budowanych przez nas sieci neuronowych możemy poprzestać na prostym schemacie neuronów oraz ich połączeń i przedstawić je tak jak w XIX wieku widział je Santiago. Dla nas neuron to przede wszystkim:

• ciało komórki
• akson - czyli "wyjście" neruonu
• dendryty - czyli "wejścia" neuronu

Dodatkowo pomiędzy aksonem jednego neuronu a dendrytami innego mamy specjalne "łączniki" zwane synapsami. Także najprostszy neuron zaprezentowano poniżej. A to akson, D to dendryty, K to ciało komórki a S to synapsy.

Mając do dyspozycji taki najprostszy neuron zobaczmy co on potrafi. Dla tych, którzy zajmowali się trochę elektroniką zamieszczony powyżej neruon może wyglądać trochę jak bramka logiczna. To dobrze, bo od prostych logicznych funkcji zaczniemy rozpoznawanie tematu sztucznych sieci neuronowych. Wydają się one najprostsze. Jednak jest pewna różnica pomiędzy bramkami a neuronami (zarówno tymi w naszej głowie jak i tymi sztucznymi). Bramki realizują tylko jedną operację zapisaną w nich na stałe. Np bramka tylko mnoży (logicznie) sygnały. Neuron umie się nauczyć. Przez to może np. mnożyć, a potem może zotać nauczony np. dodawania.
Otwartym zostaje pytanie: jak on to robi? Załóżmy więc że mamy neuron działający na dwóch wartościach 0 oraz 1. Tylko takie wartości będą na wejściu i wyjściu całego układu. Wewnątrz mogą być inne. Dodatkowo chcemy, aby nasz neuron mógł wykonać trzy najprostsze operacje logiczne: alternatywy (dodawania logicznego), koniunkcji (mnożenia logicznego) oraz negacji. Oczywiście nie będzie wykonywać tego w jednym czasie. Spróbujmy zobaczyć co musi posiadać neuron aby mógł sprostać temu zadaniu.

Ciało komórki

Sygnały ze wszystkich dendrytów "spotykają" się w ciele komórki. Co się tam z nimi dzieje? Sumują się? Mnożą? Coś innego?
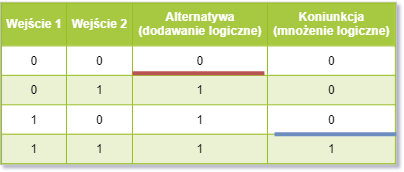
Co musiałoby się tam stać abyśmy mogli dodać i pomnożyć (logicznie) dwie zerojedynkowe wartości? Zobaczmy jak wygląda tzw. tabela prawdy dla tych dwóch funkcji:

To co możemy zauważyć na pierwszy rzut oka to identyczne odpowiedzi dla obu funkcji (każdej z osobna) w dwóch środkowych wierszach (drugim i trzecim). Co nam to daję. Otóż możemy założyć, że ciało komórki nie faworyzuje żadnego wejścia (dendrytu). Są one traktowane "równo".
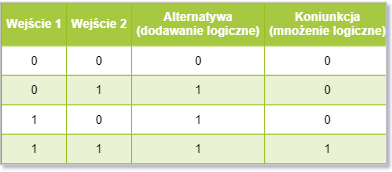
Załóżmy więc, że wartości sygnałów są przez siebie przemnożone logicznie (we wnętrzu ciała komórki). Spowoduje to oczywiście, że będzie nam działać funkcja koniunkcji. Jednak nie zadziała nam funkcja alternatywy. Jeśli dodamy (logicznie) wartości to z kolei nie zadziała nam funcka koniunkcji. Niestety jedynka na wejściu pojawia się raz wcześniej (już w drugim wierszy dla alternatywy) a raz później (dopiero w ostatnim wierszu w przypadku koniunkcji). Dla obu funkcji mamy więc jakiegoś rodzaju "progi", które sprawiają, że w którymś momencie pojawia się na wyjściu jedynka. Poniżej tabela z zaznaczonymi progami (czerwony dla alternatywy i niebieski dla koniunkcji):

Widzimy więc, że we wnętrzu ciała komórki istnieje coś co w pewnym momencie ustawia na wyjściu wartość 1 czyli przepuszcza sygnał na wyjście (akson). W przypadku sztucznych neuronów jest to tzw. funkcja aktywacji. Jaki jednak sygnał (wartość) jest na jej wejściu? Dołóżmy do naszej tabeli dodatkowe kolumny, która podpowiedzą nam co nieco. Będą to kolumny odpowiadające dodawaniu i mnożeniu arytmetycznemu. Zaznaczmy również progi jakie występują w ich wypadku. Oto co otrzymamy:

Jak widać dla zer i jedynek koniunkcja i mnożenie są identyczne (wynik i progi). Jednak dla alternatywy i dodawania mamy różnice. Otrzymujemy inne wyniki oraz dodatkowy próg (pomarańczowy). Co więcej próg zielony jest identyczny z czerwonym a pomarańczowy z niebieskim (i fioletowym). Widać więc, że operacja dodawania jest "najbogatsza" w progi. Co więc gdybyśmy to wykorzystali. Możemy więc użyć dodawania i potem przy pewnym progu aktywować neuron (przepuszczać sygnał dalej).
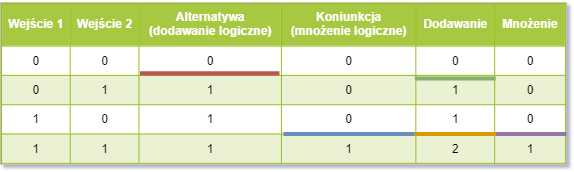
Jak może działać nasz neuron w tym momencie (aby było to dla nas wystarczające dla przeprowadzenie operacji alternatywy i koniunkcji)? Otóż dodaje on (arytmetycznie) sygnały z dendrytów, a gdy ich wartość urośnie ponad pewien próg (określony dla jego wewnętrzej funkcji aktywacji) na jego wyjściu pojawi się wartość 1. Gdy suma wejść będzie za mała akson (wyjście) będzie posiadał wartość zerową. Mamy więc na tą chwilę trzy zasady neuronu:

1. ciało komórki dodaje arytmetycznie sygnały
2. suma sygnałów przekraczająca pewien próg aktywuje neuron (i 0 na wyjściu zamienia się na 1)
3. w zależności od realizowanej funkcji próg ma inną wartość

Wszystko wygląda pięknie. Odejdźmy jednak na chwilę od funkcji logicznych i zastanówmy się co by się stało gdybyśmy chcieli zrealizować nieco inną funkcję. Np chcemy posiadać neuron z dwoma dendrytami, który aktywuje się gdy pierwszy z nich posiada sygnał, a to co jest podawane na drugim wejściu jest nieistotne. Także tabela prawdy będzie wyglądać tak:

Okazuje się, że za pomocą trzech zasad neuronu (a,b,c) zapisanych powyżej nie jesteśmy w stanie zrobić zamierzonej funkcji. Dla dwóch środkowych przypadków suma wejść jest bowiem identyczna, czyli równa 1 i neuron powinien na nie zareagować równym stanem wyjścia jeśli ma być zgodny z zasadami. Doszliśmy więc do ściany? Niekoniecznie. Okazuje się, że wiedza układu nie znajduje się w ciele komórki a poza nią. Znajduje się ona w synapsach.

Synapsa

W przypadku biologicznym jest to swego rodzaju przeszkoda dla sygnału. Swego rodzaju regulator, który przepuszcza więcej lub mniej sygnału z jednej komórki do drugiej. Używając porównania: mamy więc wiele wysp na morzu (komórek nerwowych). Na wyspę można dojachać mostem (dendryt). Każdy most ma jednak punkt poboru opłat, który przepuszcza więcej lub mniej pojazdów (synapsa).
Ta właśnie zmienna przepuszczalność pozwoli nam uzyskać neuron, który reagowałby tylko na sygnał z jednego dendrytu a był obojętny na sygnał z drugiego ("szlaban" w drugim punkcie pobory opłat będzie zawsze zamknięty).
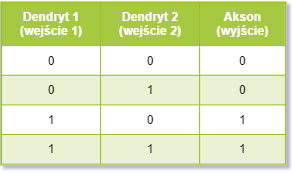
Jak zamodelujemy synapsę w przypadku naszego sztucznego systemu. Po prostu użyjemy mnożenia. Pomnożymy sygnał, który przychodzi do synapsy z innych komórek przez pewną wartość, która będzie odpowadała "przepustowości" synapsy. Będzie to pewna waga związana z każdym z wejść neuronu. Dla naszego drugiego dendrytu będzie to zero. Zatem sygnał dochodący z dendrytu do komórki możemy zapisać prostym wzorem:

Gdzie A _prev to wartość sygnału jaka przyszła od poprzedniego neuronu, a S to waga/mnożnik przypisana do każdej synapsy.
Możemy więc wykonać kolejną funkcję (trzecią). Wiemy również, że wartości każdego z sygnałów wejściowych są przemnażane na wejściu. Dochodzi nam więc czwarta zasada:

każdy z sygnałów wejściowych pochodzących od innych neronów jest przemnażany przez wagę synapsy na połączaniu z tym neuronem

Czy to koniec. Nie. Okazuje się, że możemy wyrzucić jedną z zasad i uprościć nieco nasz system. Ponieważ dzielenie to mnożenie przez liczbę odwrotną, a my każdy z sygnałów na wejściu mnożymy, możemy podzielić wszystkie wagi synaps przez wartość progu aktywacji neuronu. Co nam to da? Otóż próg aktywacji będzie miał wtedy zawsze wartość 1. Oznacza to, że rozważane przez nas dotychczas funkcje możemy zrealizować przyjmując następujące zasady neuronu:

1. ciało komórki dodaje arytmetycznie sygnały
2. suma sygnałów przekraczająca 1 aktywuje neuron (i 0 na wyjściu zamienia się na 1)
3. każdy z sygnałów wejściowych pochodzących od innych neronów jest przemnażany przez wagę synapsy

Pamiętajmy, że jest to zbiór zasad jaki pozwala nam na realizację rozważanych do tej pory funkcji.
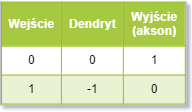
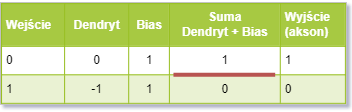
Wróćmy jednak do zapomnianej negacji. Jest ona jeszcze prostszą funcką niż omawiane wcześniej. Czy uda nam się ją zaimplementować za pomocą naszego neuronu. Jaką wartość powinna mieć waga synapsy abyśmy spełnili następującą tablicę prawdy:

Jeśli zastanawiasz się dlaczego wyjście jest opisane jako akson, a wejście nie jest już opisane jako dendryt to jest tak dlatego, że wprowadziliśmy synapsy, które są przed dendrytami. Także dendryt i wejście nie oznaczają teraz tego samego.
Co do negacji, która musi "odwracać" wartość sygnału. Jak tego dokonać? Otóż musimy zastosować odwrotność (liczbę odwrotną). Ustawiamy wartość wagi synapsy na odwrotność 1 czyli: -1. Otrzymamy wtedy sumę dendrytów równą -1 (dla jednego przypadku) lub 0 (dla drugiego):

Niestety przy założeniu (B), że suma sygnałów dopiero po przekroczeniu wartości 1 aktywuje neuron nie osiągniemy pożądanych wartości wyjściowych. U nas jest tylko jeden dendryt czyli jego sygnał równa się sumie tego co pójdzie do ciała komórki. Dodatkowo maksymalna wartość dla tego dendrytu to 0. Co więc robimy? Możemy rozluźnić założenia co do funkcji aktywacji. Możemy aktywować ją przy różnych progach. Jednak pójdziemy drugą drogą, aby nasz neuron posiadał to co ma każdy "szanujący się" sztuczny neuron, czyli tzw. bias.

Bias

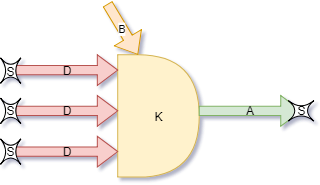
Jak widać na powyższej tabeli, gdybyśmy wartością sygnałów jakie ma dendryt dodali po 1 (w każdym wierszu) osiągnęli byśmy neuron realizujący funkcję negacji. I to w dużym skrócie jest zadanie biasu. Jest on dodatkowym dendrytem, który dodaje pewną stałą wartość do sumy sygnałów przychodzących do ciała komórki ze wszystkich "normalnych" dendrytów. Możemy więc zmodyfikować nieco schemat naszego prostego neuronu:

Rozwińmy też naszą tabelę wartości, aby zobaczyć co się dzieje wewnątrz neuronu. Dodatkowo próg aktywacji zaznaczymy czerwoną linią:

Należy pamiętać, że wartość jaką dodaje bias nie zawsze musi być 1. Jeśli chcielibyśmy aby nasz neuron znów wykonywał dodawanie lub mnożenie musielibyśmy użyć innych wartości. Aby umożliwić "płynną" zmianę tej wartości musimy dodać do biasu synapsę. W końcu denryty (a nim jest bias) są jedynie przekaźnikami sygnału z synapsy do ciała komórki i same nic z nim nie "kombinują" ani nie zmieniają swojego zachowania (zgodnie z zasadami dziłania neuronu, które do tej pory spisaliśmy). Jaki sygnał wejściowy będzie miała ta biasowa synapsa (w końcu jest to "ślepe" wejście nie przychodzące z żadnego innego neuronu)? Dla uproszczenia zakłada się, że będzie to najprostsza do mnożenia liczba: 1.

Podsumowanie

Doszliśmy więc do neuronu, który potrafi wykonać kilka podstawowych funkcji w zależności od tego jakie wagi ustawione są na jego wejściwoych synapsach. Ostateczny schemat sztucznego neurony na tym etapie wygląda następująco:

Może to być nieco skąplikowane, ale nie jest. Jeszcze raz opiszmy sobie wszystkie symbole na schemacie (tak dla pewności):

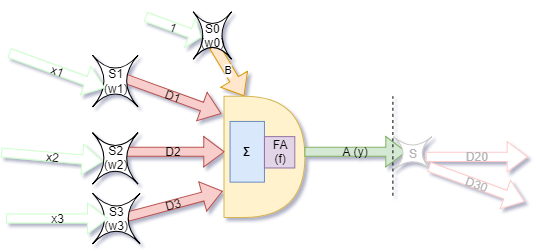
• x1, x2, x3 - są to wartości sygnałów które przychodzą do synaps wejściowych naszego neuronu
• 1 - wartość stała sygnału podawanego na bias
• S0, S1, S2, S2 - są to synapsy wejściowe naszego neurony, które posiadają wagi liczbowe
• w0, w1, w2, w3 - są to wartości liczbowe wag synaps wejściowych naszego neuronu
• D1, D2, D3 - są to dendryty
• B - bias (dodatkowy dendryt)
• Σ - umowny sumator znajdujący się na wejściu ciała komórki i dodający sygnały ze wszystkich dendrytów
• FA - funkcja aktywacji (zapisywana także jako f) - funkcja przeliczająca wartość z sumatora na sygnał podawany na wyjście neuronu. W najprostszym przypadku zmienia 0 na 1 po przekroczeniu przez sumę pewnego progu
• A - akson (wyjście) neuronu
• y - wartość sygnału w aksonie

Interesuje nas wszystko na lewo od przerywanej linii. Po prawej jej stronie zaznaczyłem następną synapsę i dendryty następnych neuronów. W końcu one są połączone jeden za drugim.
Skoro mamy tyle symboli, to na koniec przydałby się jakiś wzorek ;-)
Jak nietrudno się domyślić będziemy wyznaczać y w zależności od x (i innych wartości). Wzór na sygnał wyjściowy neuronu wygląda następująco:


Także tym pięknym wzorem kończymy ten wpis. Mam nadzieję, że następny nie będzie trzeba tyle czekać ile na ten ;-)